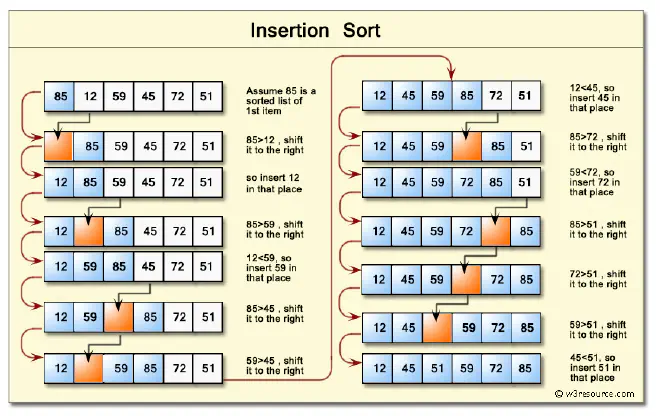
Insert Sort

Table of Contents

Elixir DSA - This article is part of a series.

Part 2: This Article

Insert sort is the defacto algorithm most programmers get started on their journey with. Lets see how to implement it in Elixir.

Understanding the Algorithm

Insert sort works by maintaining 2 lists. A sorted_list and an unsorted_list. We iterate through each item in the unsorted_list, comparing it with elements in the sorted_list, and inserting it into the correct position.

Here’s a step by step breakdown-

Initially, the entire list is unsorted, and the sorted_list is empty.
We start by considering the first element of the unsorted_list as sorted(Since a single element list is always sorted). This becomes our sorted_list.
We then move to the second element and insert it into the correct position in our sorted_list by comparing it with the existing element(s).
This process continues until we’ve inserted every element from the unsorted_list into the sorted_list

If that flew right over your head, no worries.

Here’s a flow diagram to visualise it.

graph TD Start([Start]) --> Init[["Initial Array: [5, 2, 4, 6, 1, 3]"]] Init --> Step1["Step 1: Compare 2 with 5 Swap: [2, 5, 4, 6, 1, 3]"] Step1 --> Step2["Step 2: Compare 4 with 5, then 2 Insert 4: [2, 4, 5, 6, 1, 3]"] Step2 --> Step3["Step 3: 6 is in correct position No change: [2, 4, 5, 6, 1, 3]"] Step3 --> Step4["Step 4: Compare 1 with all previous Insert 1: [1, 2, 4, 5, 6, 3]"] Step4 --> Step5["Step 5: Compare 3 with previous Insert 3: [1, 2, 3, 4, 5, 6]"] Step5 --> Final["Final Sorted Array: [1, 2, 3, 4, 5, 6]"] Final --> End([End])

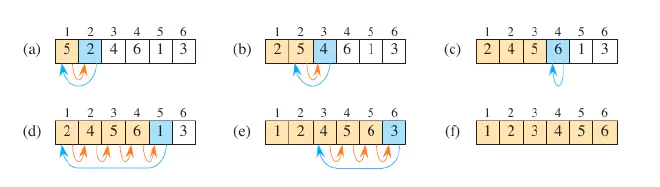
Insert Sort Step 1 — A demonstration of insert sort

It’s helpful to visualize this as two separate lists: [sorted_list, unsorted_list]. With each iteration, the sorted_list grows while the unsorted_list shrinks.

I’ve attached a helpful video at the end to make it clearer.

The Elixir twist

Here’s where Elixir adds an interesting twist: it’s an immutable language. Instead of swapping elements within the same array, we’ll create a new sorted_list and insert elements into it accordingly. This approach aligns perfectly with Elixir’s functional programming paradigm.

Implementation

The `Sort/1`

First, we’ll define a sort/1 function with a guard clause to ensure we’re working with a list. It takes the unsorted_list and passes it on to the do_sort/2 function, along with an empty list(oursorted_list, which is initially empty)

def sort(list) when is_list(list), do: do_sort(list, [])

The `do_sort/2`

The do_sort/2 function is where the magic happens. As explained, we want to maintain an unsorted_list and a sorted_list, compare each element, and add it at the right place. do_sort/2 takes the first argument as the unsorted_list, the second as the sorted_list. We want to pattern match the unsorted_list with the head | tail operator and compare each head with the items in the sorted_list, then insert accordingly. Then, it must recursively call itself with the tail.

Lets write the exit-case for the do_sort/2 function. Our job is done when the first argument – the unsorted_list is empty and all the elements have been sorted. This is when our sorting is complete. In this case, we just need to return the sorted_list – this is what breaks us out of the recursion loop.

Let’s pattern match the first argument with an empty list, the second with the sorted_list, then return the sorted_list

def do_sort([], sorted), do: sorted

Then comes the fun part. The do_sort/2 function must compare the head each time, use a helper function to insert the head into the correct position of the sorted_list, then recurse itself. The second time, the tail becomes the unsorted_list and we again pass it as the first argument to the do_sort/2 function.

def do_sort([head | tail], sorted), do: do_sort(tail, insert(head, sorted))

That helper function will be the insert/2 function. It should take 2 arguments. First – which element to insert, and second – the sorted list(which list to insert in).

The `insert/2`

This time, lets write the entry case. That is, if our sorted_list is empty – as will be the first time we call insert/2, we simply return the item in an empty list. Let’s pattern match the sorted_list to an empty list, and return the single item in a list.

 def insert(item, []), do: [item]

Let’s cover the other cases next.

We want the insert function to compare the item with the head each time and do one of 2 things -

If the item is smaller than head, prepend it to the list. This is done by adding a guard that checks if item <= head

def insert(item, [head | tail]) when item <= head, do: [item, head | tail]

If the item is larger than head, it must recurse itself and compare it with the next element of the sorted list. We leave the head as is, and call insert with the item and the tail. This loops until the above condition of item <= head is matched, at which point it inserts the item into the list.

def insert(item, [head | tail]), do: [head | insert(item, tail)]

And that’s it! We have a working insert sort algorithm written in Elixir!

Observe the caveats here. Elixir being a functional programming lanugage, we’ve avoided the use of for-while loops & if-else statements as much as possible. There are a few named functions, each with different arities, that pattern match and call each other multiple times with recursion. This forms the crux of functional programming in Elixir.

Here’s the final code - Give it a try in your iex!

defmodule InsertionSort do
  def sort(list) when is_list(list), do: do_sort(list, [])

  def do_sort([], sorted), do: sorted
  def do_sort([head | tail], sorted), do: do_sort(tail, insert(head, sorted))

  def insert(item, []), do: [item]
  def insert(item, [head | tail]) when item <= head, do: [item, head | tail]
  def insert(item, [head | tail]), do: [head | insert(item, tail)]
end