Quick Sort

Quick Sort is the go-to sorting algorithm for many programmers due to its efficiency and elegance. Lets implement it in Elixir-

Understanding the Algorithm

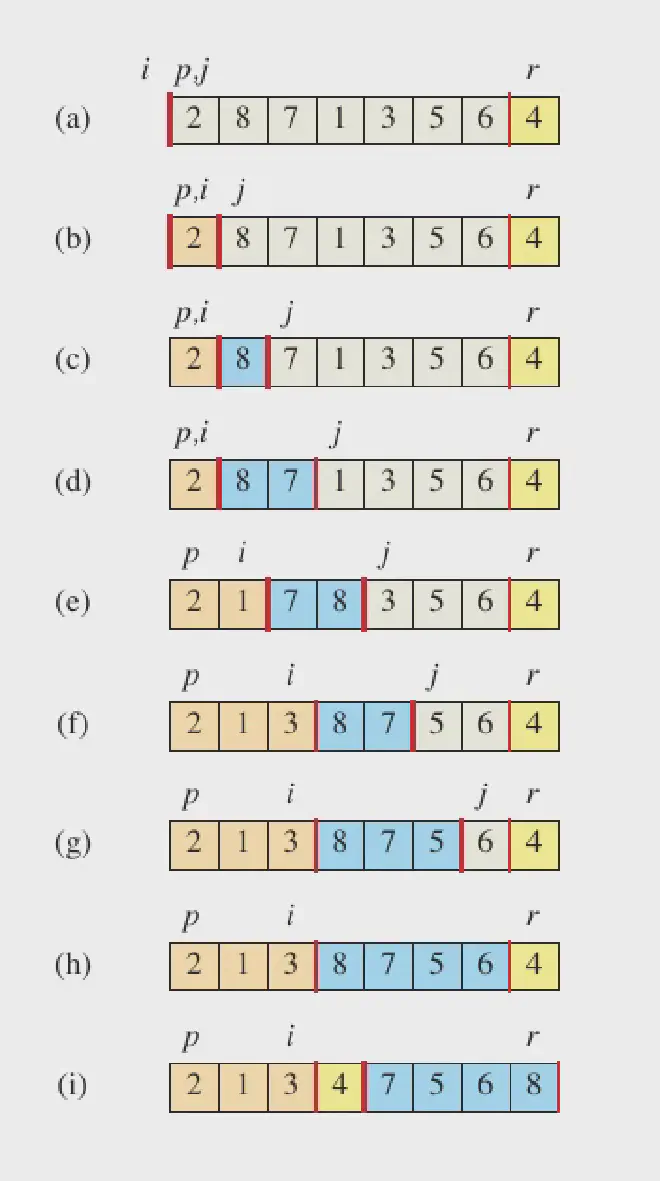
Quicksort works on the principle of “divide and conquer”. It picks an element as the ‘pivot’ and partitions the list around it. The goal is to put the pivot in its correct position in the sorted list.

Here’s a step by step breakdown:

1. Choose an element from the list as the pivot(usually the first element).
2. Partition(rearrange) the list so that all elements smaller than the pivot are on its left, and all elements greater are on its right.
3. Then the pivot is in its correct position.
4. Recursively apply steps 1-2 to the sub-lists on the left and right of the pivot.

Here’s a flow diagram to visualize it:

I’ve attached a helpful video at the end to make it clearer.

The Elixir twist

Elixir is an immutable language. Although technically possible to swap the positions of elements and get lists, we’ll take a slightly different approach. Instead of swapping the elements in the same list, we’ll add them to a new list, and recurse on them.

So here’s the modified algorithm for Elixir -

1. We choose a pivot - the first element of the array(same as before)
2. We iterate through the list, while maintaining 2 lists - one with all elements greater than the pivot(left_list), another with all elements less than the pivot(right_list) .
3. We then recurse on both these lists while prepending & appending them to the pivot.

The implementation will make it clearer-

Implementation

The sort/1

Lets define our main sort/1 function. Its the brains behind the quick-sort algo. First, it must take the input list & calculate the pivot. Then split the input list into 2 lists - one with all elements greater than the pivot, another with all elements less than the pivot. Then use recursion on the 2 lists while assembling the sorted list.

Quite a lot for a single function to do!

For the splitting, we’ll make use of the Enum.reduce/3. We’ll maintain a tuple containing the left & right lists(the accumulator), and define another helper function that appends each element to the left/right list according to which is greater(the pivot or the element).

def sort(list) do
  pivot = hd(list)
  {left_list, right_list} = Enum.reduce(list, {[], []}, &function(&1, &2, pivot))
  sort(left_list) ++ [pivot] ++ sort(right_list)
end

Here, the initial acc is the tuple containing both the empty lists. The helper function returns the tuple containing the modified left, right lists, which becomes the acc for the next iteration.

Finally, we pattern match the left and right lists returned by the reduce and recurse on them as sort(left_list) ++ [pivot] ++ sort(right_list) (since the pivot is in its correct position, all the elements to its left are less than it and unsorted, all elements to its right are greater than it and unsorted.)

Lastly, we need to handle the base case - when one of the lists will be empty(as will be when we reach the ending stages). We just want to return and empty list in that case. That’s a one-liner-

def sort([]), do: []

With that, we’ve finished most of the heavy lifting. All thats left is to define a helper function that appends each element to the left/right list if its greater/less than the pivot.

The function/3

With that, lets come to our helper function. It must take 3 arguments - the element to compare, the tuple containing the left and right lists, and the pivot. We want to compare each element with the pivot and do one of three things -

1. If element less than pivot: We want to append the element to the left_list(list containing all elements less than pivot)
2. If element greater than pivot: We want to append the element to the right_list(list containing all elements greater than pivot)
3. If element equal to pivot: We’d want to return both the lists as is(Since the pivot is already taken care of) The comparisons can be carried out with suitable guards.

def function(x, {left_list, right_list}, pivot) when x > pivot do
  {left_list, right_list ++ [x]}
end

When the element (x) is greater than the pivot, we’re appending it to the right_list and returning the tuple.

def function(x, {left_list, right_list}, _) do
  {left_list ++ [x], right_list}
end

In the case when element is less, we append it to the left_list.

Lastly, when we encounter the pivot, we want to return the tuple as is since the pivot has already been added to the sorted list.

def function(x, acc, pivot) when x == pivot do
  acc
end

And thats it! We’ve implemented quicksort in Elixir!

Once again, I’d ask you to observe the caveats here. Elixir being a functional programming lanugage, we’ve avoided the use of for-while loops & if-else statements. There are just 2 named functions, each with different arities, that pattern match and call each other multiple times with recursion. This forms the crux of functional programming in Elixir.

Here’s the final code- Give it a try in your iex!

defmodule Quicksort do
  def sort([]) do
    []
  end

  def sort(list) do
    pivot = hd(list)
    {left_list, right_list} = Enum.reduce(list, {[], []}, &function(&1, &2, pivot))
    sort(left_list) ++ [pivot] ++ sort(right_list)
  end

  def function(x, acc, pivot) when x == pivot do
    acc
  end

  def function(x, {left_list, right_list}, pivot) when x > pivot do
    {left_list, right_list ++ [x]}
  end

  def function(x, {left_list, right_list}, _) do
    {left_list ++ [x], right_list}
  end
end

Visualization